Support vector machines are a super star in machine learning and data mining in the past decade. It reheats statistical learning in machine learning community. It is also one of the classifiers that work practically with applications to other disciplines such as bioinformatics.
In this post, I will give a brief review of the theory of this classifier and show an F# implementation using the quadratic programming (QP) solver in Microsoft Solver Foundation (MSF).
It may seem dull to start with mathematics. But the math in SVMs is actually quite intuitive and would be quite easy if one has some training in linear algebra and calculus. Also understanding the intuition behind the formulae is more important in the formulation itself. There are quite a lot of good SVM tutorials written by researchers. Thus I only write the important formulas that occur in the implementation. The reader could link the F# code with formulas directly.
My note is based on the machine learning course by Prof. Jaakkola [Jaakkola] and the Matlab implementation therein. The course material is highly comprehensive yet accurate.
Background review for SVMs
Given a binary labeled dataset, where
and
is 1 or -1. Think about the data points
plotted in a d dimensional (Euclidean) space, the linear SVM classifier is a hyperplane
in the space and it “best” separates the two kinds of data points. Here “best” means that the hyperplane should have the largest margin, which is the distance from the plane to the sides of labeled points. Intuitively the larger the margin is, the more robust and confident the classifier is. As if the hyperplane shakes a little, it still classifies well for its being far from both sides.
Let’s take d=2 as the discussing example: data points are plotted in a 2-D plane. The aim is to draw a line
to separate the two kinds of points such that the margin of the separation is maximized. In the following Figure, the line with maximum margin is shown. After some geometry work, the margin is calculated as
, thus minimizing
with the constraints that the two kinds of points are well separated (
) gives the max-margin hyperplane.
(Wikipedia picture)
Two important extensions to the above simplest SVM are:
1. Allowing imperfect separation, that is when a hyperplane could not separate the points perfectly, it is allowed to mis-separate some data points. This introduces a slack variable for each data point
, when the point is on the correct side of the plane, the slack variable is 0, otherwise it is measures the distance it goes from the plane minus 1, if the values goes to below zero set it zero. (Please read the Note and reference section for more explanation.)
2. Kernel. The simplest SVM is a linear classifier in the original space. However, there are situations where linear classifier is not sufficient (even the best), one strategy is to do a non-linear transformation or mapping that maps a data point
to another space, so that a linear classifier in that space, which is non-linear in the original
space, does a better separation of the data points. The kernel trick is that we don’t need to define
explicitly; only the definition of inner product of that space is required:
.
With the two extensions, the new maximum margin objective becomes:
subject to
The dual form:
subject to
The data points with its alpha value greater than 0 are called support vectors.
With the in the dual problem solved, the SVM classification hyperplane is recovered by:
The threshold parameter could be calculated by substituting back to the support vectors:
Any and
(So that make sure data point
is on the margin boundary, not in-between) would give a
, to stabilize the solution, it is common practice to take the median of off the possible
.
The implementation
The solver is actually an Interior Point Solver, which could solve linear and quadratic programming with linear constraints.
Page 14-17 of MSF-SolverProgrammingPrimer.pdf show an example usage of the QP solver in Microsoft Solver Foundation. But the example is not complete and it does not demonstrate one very subtle part: how to set the coefficients for the quadratic terms.
The following code example shows a simple example with the the comment regarding the coefficient setting:
- #r @"C:\Program Files (x86)\Sho 2.0 for .NET 4\packages\Optimizer\Microsoft.Solver.Foundation.dll"
- open Microsoft.SolverFoundation.Common
- open Microsoft.SolverFoundation.Solvers
- open Microsoft.SolverFoundation.Services
- // test QP
- module TEST =
- (* minimize x^2 + y^2 + 3xy + 2x + y *)
- (* notice that in the InteriorPointSolver,
- the coefficients for xy & yx should be the same (so only set ONCE!)
- if we set both 3xy and 0yx, the solver takes the later coef.
- *)
- let solver = new InteriorPointSolver()
- let _, goal = solver.AddRow("dual objective value")
- solver.AddGoal(goal, 0, true)
- let _, x = solver.AddVariable("x")
- let _, y = solver.AddVariable("y")
- solver.SetCoefficient(goal, x, Rational.op_Implicit(2))
- solver.SetCoefficient(goal, y, Rational.op_Implicit(1))
- // for terms like x-y (where x != y), set its coef for only one time!
- solver.SetCoefficient(goal, Rational.op_Implicit(3), x, y)
- //solver.SetCoefficient(goal, Rational.Zero, y, x)
- solver.SetCoefficient(goal, Rational.op_Implicit(1), x, x)
- solver.SetCoefficient(goal, Rational.op_Implicit(1), y, y)
- let param = new InteriorPointSolverParams()
- solver.Solve(param) |> ignore
- //solver.Result
- let objectiveValue = solver.GetValue(0).ToDouble()
- let x0 = solver.GetValue(1).ToDouble()
- let y0 = solver.GetValue(2).ToDouble()
- x0*x0 + y0*y0 + 3.0 * x0 * y0 + 2. * x0 + y0
- //x0*x0 + y0*y0 + 0.0 * x0 * y0 + 2. * x0 + y0
The implementation of SVM is a straightforward translation of equations (1) to (5). The following shows the svm learning (bulidSvm) and testing (svmClassify) functions:
- open System
- type dataset =
- { features: float array array; // (instance = float array) array
- mutable labels: int array; //
- }
- with
- member x.NumSamples = x.features.Length
- module Array =
- let median (a:'a array) =
- let sorted = Array.sort a
- sorted.[sorted.Length / 2]
- module Kernel =
- let linear a b =
- Array.fold2 (fun acc p q -> acc + p * q) 0.0 a b
- let polynomial k a b =
- let dot = linear a b
- Math.Pow(1.0 + dot, k |> float)
- let gaussian beta a b =
- let diff = Array.fold2 (fun acc p q -> acc + (p-q)*(p-q)) 0.0 a b
- exp (-0.5 * beta * diff)
- module SVM =
- type svmmodel = {
- SVs:dataset;
- alpha:float array;
- kernel: float[] -> float[] -> float;
- w0:float;
- }
- with
- member x.NumSupporVectors = x.SVs.features.Length
- let buildSVM (ds:dataset) (C:float) (kernel:float[] -> float[] -> float) =
- let n = ds.features.Length
- let C = Rational.op_Implicit(C)
- let zero = Rational.Zero
- // create a interior point solver, which solves the QP problem
- let solver = new InteriorPointSolver()
- // set the objective value / goal
- let _, goal = solver.AddRow("dual objective value")
- // false == maximizing the objective value
- // the value of goal is (1)
- solver.AddGoal(goal, 0, false) |> ignore
- // add the Lagangian variables \alpha_i and set their bounds (0 <= \alpha_i <= C)
- let alpha = Array.create n 0
- for i=0 to n-1 do
- let _, out = solver.AddVariable("alpha_"+i.ToString())
- alpha.[i] <- out
- solver.SetBounds(out, zero, C)
- // add contraint: \sum_i \alpha_i * y_i = 0
- // equation (2)
- let _, sumConstraint = solver.AddRow("SumConstraint")
- solver.SetBounds(sumConstraint, zero, zero);
- for i=0 to n-1 do
- // set the coefs for the sum constraint
- // equation (2)
- solver.SetCoefficient(sumConstraint, alpha.[i], Rational.op_Implicit(ds.labels.[i]))
- // add the \alpha_i terms into the objective
- solver.SetCoefficient(goal, alpha.[i], Rational.One)
- // add the qudratic terms
- for j=0 to i do
- // coef = y_i * y_j * K(x_i, x_j)
- let coef = float(ds.labels.[i] * ds.labels.[j]) * (kernel ds.features.[i] ds.features.[j])
- if i=j then
- solver.SetCoefficient(goal, Rational.op_Implicit(-0.5 * coef), alpha.[i], alpha.[j])
- else
- solver.SetCoefficient(goal, Rational.op_Implicit(-coef), alpha.[i], alpha.[j])
- // use the default parameters
- let param = new InteriorPointSolverParams()
- solver.Solve(param) |> ignore
- // get the alpha values out
- let alphaValue = Array.init n (fun i -> solver.GetValue(i+1))
- (* print optimization result
- printfn "goal value = %A" (solver.GetValue(0).ToDouble())
- for i=1 to n do
- printfn "%A" (solver.GetValue(i).ToDouble())
- *)
- let alphaNew = new ResizeArray<Rational>()
- // extract the non-zero alpha values out and their corresponding support vectors
- let SVs =
- let feats = new ResizeArray<float[]>()
- let labs = new ResizeArray<int>()
- let maxAlpha = Array.max alphaValue
- let threshold = maxAlpha * Rational.op_Implicit(1e-8)
- for i=0 to n-1 do
- if alphaValue.[i] > threshold then
- feats.Add(ds.features.[i])
- labs.Add(ds.labels.[i])
- alphaNew.Add(alphaValue.[i])
- { features = feats |> Seq.toArray;
- labels = labs |> Seq.toArray;
- }
- // solve w_0 in the primal form
- let alphaNZ = alphaNew |> Seq.toArray
- // equation (5)
- let w0 =
- alphaNZ
- |> Array.mapi (fun i a ->
- if a = C then
- None
- else
- let mutable tmp = 0.0
- for j=0 to SVs.NumSamples-1 do
- tmp <- tmp + alphaNZ.[j].ToDouble() * (SVs.labels.[j] |> float) * (kernel SVs.features.[i] SVs.features.[j])
- Some ((float SVs.labels.[i]) - tmp)
- )
- |> Array.filter (fun v -> match v with None -> false | _ -> true)
- |> Array.map (fun v -> match v with Some v -> v | _ -> 0.0)
- |> Array.median
- // construct an svm record
- {
- SVs = SVs;
- alpha = alphaNZ |> Array.map (fun v -> v.ToDouble());
- kernel = kernel;
- w0 = w0;
- }
- let svmClassify (model:svmmodel) (ds:dataset) =
- // equation (4)
- let vals =
- ds.features
- |> Array.map (fun x ->
- let mutable sum = 0.0
- for i=0 to model.NumSupporVectors-1 do
- sum <- sum + model.alpha.[i] * (float model.SVs.labels.[i]) * (model.kernel model.SVs.features.[i] x)
- sum + model.w0
- )
- let nCorrect =
- Array.map2 (fun value label -> if (value > 0.0) && (label = 1) || (value < 0.0) && (label = -1) then 1 else 0) vals ds.labels
- |> Array.sum
- (float nCorrect) / (float ds.NumSamples), vals
Try on the iris data set we used in the Logistic Regression post:
let svm = buildSVM iris 10.0 Kernel.linear
let classifyResult = svmClassify svm iris
val svm : svm =
{SVs =
{features =
[|[|1.0; 6.2; 2.2; 4.5; 1.5|]; [|1.0; 5.9; 3.2; 4.8; 1.8|];
[|1.0; 6.3; 2.5; 4.9; 1.5|]; [|1.0; 6.7; 3.0; 5.0; 1.7|];
[|1.0; 6.0; 2.7; 5.1; 1.6|]; [|1.0; 5.4; 3.0; 4.5; 1.5|];
[|1.0; 4.9; 2.5; 4.5; 1.7|]; [|1.0; 6.0; 2.2; 5.0; 1.5|];
[|1.0; 6.3; 2.7; 4.9; 1.8|]; [|1.0; 6.2; 2.8; 4.8; 1.8|];
[|1.0; 6.1; 3.0; 4.9; 1.8|]; [|1.0; 6.3; 2.8; 5.1; 1.5|];
[|1.0; 6.0; 3.0; 4.8; 1.8|]|];
labels = [|-1; -1; -1; -1; -1; -1; 1; 1; 1; 1; 1; 1; 1|];};
alpha =
[|6.72796421; 10.0; 10.0; 10.0; 10.0; 6.475497298; 1.490719712;
8.547262902; 3.165478894; 10.0; 10.0; 10.0; 10.0|];
kernel = <fun:svm@226-32>;
w0 = -13.63716815;}
>
Real: 00:00:00.002, CPU: 00:00:00.000, GC gen0: 0, gen1: 0, gen2: 0
val classifyResult : float * float [] =
(0.97,
[|-2.787610618; -2.380530973; -1.42477876; -2.929203541; -1.681415929;
-1.96460177; -1.24778761; -6.106194692; -2.761061946; -2.973451328;
…. 4.203539824; 1.82300885|])
Notes and references
The optimization in SVMs could be treated as a general QP problem as shown in our implementation. However, when the number of the data points is big, the QP grows too big to handle by the QP solver.
As a special QP problem, SVM has a lot of novel solutions proposed in the machine learning research area, e.g. the SMO approach [Platt] in LibSVM implementation and the Ball Vector Machine approach [Tsang] transforming the special QP into a (discrete) computational geometry problem, minimum enclosing ball. For practical usage of SVM, one usually uses these dedicated approaches.
Besides the maximum margin interpretation, SVMs also have theory roots in functional regularization theory, in which the optimization
is viewed as minimizing the error term while controlling the complexity of the function
and C is a tradeoff parameter between these two. The reader is referred to the teaching notes and papers by Prof. Poggio [Poggio].
[Burges] A Tutorial on Support Vector Machines for Pattern Recognition. http://research.microsoft.com/en-us/um/people/cburges/papers/svmtutorial.pdf
[Jaakkola] http://courses.csail.mit.edu/6.867/.
[Platt] Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines. ftp://ftp.research.microsoft.com/pub/tr/tr-98-14.pdf
[Poggio] http://www.mit.edu/~9.520/spring10/.
[Tsang] http://www.cs.ust.hk/~ivor/cvm.html.




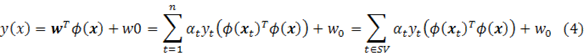
![clip_image002[5] clip_image002[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiBgyzSXqw_Dlm-mONey3s9HxNY9TQqL8dHnRuvgJXLZUJuYAQ1rnJGmceMcnXcY40hYH0t-Dx3Fw1aEt3GUDvOgQeKnjLc7-IG1IShvl6Kp_vkBkH6CDO9GS8BT4hBATSV9r3LPR7saYn_/?imgmax=800)
![clip_image006[3] clip_image006[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhjz27zB5In4AP1BltKNswA60dACWiMjG-EH3y0x8qDOB-o2y8_b0lOPm7zqHSrt43tyQjkD_v5aqit3ni_PA1jEBMho-GJYtyayrvCydEqi5vSiCPpWfc3bdrbDfWjtyzolG0qgLsjZJN6/?imgmax=800)
![clip_image010[1] clip_image010[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiXwknve9QSN-0t6pVDnlkdpZH2ROt0lng_oAMdLBMwLtlQIctaa_0mmmDBX_PVcG89ZjPDbHJiEGtJL84FIzFhWBUlrpCML56ILImeFgL6wYgHXZNfIBeVK2uG5x1udozcNwoYtbJ9OGRN/?imgmax=800)