Yin Zhu
14 September 2011
(The code for this article is at codeplex.)
Binary search trees play an extremely important role in computer science. They were hot research topics back to 1970s and early 1980s. While the plain binary search tree is of little usage, balanced search trees are now being used everywhere. For example, most C++ STL implementations use Red Black Tree for its set and map containers. The F# Core library uses a functional version of AVL tree for Set and Map, which are both persistent/functional containers.
Special binary search trees also have other functionalities other than implementing standard set or map containers. For example, splay tree has an efficient split operation – splitting a dynamic set into two in O(log n) time: one is less than the given key; the other is greater than or equal to the given key. This operation could be used to optimize network flow algorithms. Details could be found in Tarjan’s classical (also tiny) data structures book published in 1983.
In this post, I’d like to implement the classical Red Black Tree in F#. I searched on the internet and found that there were some Red Black Tree code snippets in F#, but none of them are complete. Some only implemented the insert operation, which is relatively easy. Some are incorrect.
My main purpose for implementing the Red Black Tree in F# is to test whether I am still good at implementing complex data structures (I implemented quite a few classical data structures and algorithms during my early undergraduates for ACM/ICPC competitions). But there are new things: 1) the implementation language is F# rather than C++, 2) the implementation should be functional rather than imperative, and 3) the interface design should be general, and allows code reuse.
One function I always miss from standard set containers is dynamic order statistics – finding the ith smallest element in a dynamic set. The query time should be in O(log n). To accomplish this, we need add a size field to the internal tree node. Adding extra fields into a data structure is called augmenting data structures (Chapter 14, CLRS). Augmenting data structures is useful when a function is not built in a classical data structure but can be added by genuinely modifying the classical data structure. It is a very important skill when solving algorithmic competition problems.
I divided this article into several sections. I will first introduce the basics of red black trees, and then we move the insertion part, and order statistics, and then the hardest part – deletion. I have a section describing the testing procedures that ensure the correctness of the implementation. At last, I will leave the specifics of Red Black Trees, and cover the tree traversal in general and show some more functional stuff: continuation and a continuation Monad.
Red Black Tree Basics
A Red Black Tree is a binary search tree with the following extra properties:
1. The root is black and the leaf nodes are black (note: leaf nodes do not contain keys, only internal nodes contain keys).
2. A red node’s two children must be black.
3. For any subtree rooted at x, all the simple paths down to the leaf nodes contain the same number of black nodes.
With the above properties, the Red Black tree is able to perform queries such as search, insert and delete all in O(log n) time.
The F# definition of the tree is given below:
type Color =
Red | Black | DoubleBlack
type RBTree<'a when 'a:comparison> =
| Node of Color * 'a * int * RBTree<'a> * RBTree<'a>
| Leaf of Color
Notice that a node could be Red or Black. For black, there are two cases Black and DoubleBlack. The DoubleBlack color is used only when we are dealing with deletion, and in a valid Red Black tree, there would be of no DoubleBlack node. I will explain DoubleBlack in the delete section.
A Red Black Tree has two kinds of nodes: internal nodes storing keys and dummy leaf nodes. The internal node has a color field, the key filed, the size of the subtree and left and right children. The leaf node has two possible colors: Black or DoubleBlack.
Let’s write two simple recursive functions working on the tree structure to get us warmed up:
let rec contains x = function
| Leaf _ -> false
| Node (_, y, _, a, b) ->
if x = y then true
elif x < y then contains x a
else contains x b
let rec depth = function
| Leaf _ -> 0
| Node (_, _, _, a, b) ->
1 + max (depth a) (depth b)
The first is to test whether a key x is in the tree or not. The second is to calculate the depth of a tree.
Insert
For insertion, there is a known trick found by Chris Okasaki in this paper (Red-black trees in a functional setting). Okasaki is also the author of the famous book, Purely Functional Data Structures.
The idea of insertion is: always insert a Red node at some leaf node so that property 3 holds, then fix property 2 up to the root. There are four cases where property 2 could break. For all the four cases, the grand parent is always black, and there will be two red nodes right in the below. Please see the picture on page 3 of the paper.
Then the buttom-up fixing goes up the root. The root may be changed into Red. To hold property 1, simply change the color of the root to Black.
let insert x (t: RBTree<'a>) =
let balance = function
| Black, z, size, Node (Red, y, _, Node (Red, x, _, a, b), c), d
| Black, z, size, Node (Red, x, _, a, Node (Red, y, _, b, c)), d
| Black, x, size, a, Node (Red, z, _, Node (Red, y, _, b, c), d)
| Black, x, size, a, Node (Red, y, _, b, Node (Red, z, _, c, d))->
Node (Red, y, size, Node (Black, x, (getSize a b)+1, a, b), Node (Black, z, (getSize c d)+1, c, d))
| color, b, _, c, d -> // grandparent is red, does not change
Node (color, b, (getSize c d)+1, c, d)
let rec ins = function
| Leaf _ ->
Node (Red, x, 1, Leaf(Black), Leaf(Black))
| Node (color, y, size, a, b) as s ->
if x < y then balance(color, y, (getSize a b)+2, ins a, b)
elif x > y then balance(color, y, (getSize a b)+2, a, ins b)
else s
match ins t with
| Node (Red, y, size, a, b)->
Node (Black, y, size, a, b)
| t -> t
Order statistics
Let’s have some rest before going to the monstrous delete operation. To get the nth smallest key in the tree, we can add a size field to each node, which is the size of the subtree rooted at the node. Thus the size of Node(_, _, _, left, right) is defined as
size = left.size + right.size + 1
and, as a boundary condition, a leaf node has size 0.
With this size field, the nth function is given below:
let nth n t =
let rec nth' n = function
| Leaf _->
failwith "can't find the nth member"
| Node (_, v, size, l, r)->
let lsize=getSize l (Leaf(Black))
if lsize+1=n then
v
elif lsize+1>n then
nth' n l
else
nth' (n-lsize-1) r
if n >= size t || n < 0 then
failwith "nth out of range"
else
nth' (n+1) t
Delete
The idea of delete is simple (if we don’t care about the three properties of Red Black Trees): if the node x to be deleted has less than two children, then simply delete it, and lift its child (if any) to its position; if the node has two children, that means there must a node that is just bigger than x in its right child, replace x with that value, now the problem reduces to delete the smallest node in x’s right child.
First let’s write the function to get the smallest value in a tree:
let rec min = function
| Leaf _->
None
| Node (_, value, _, Leaf(Black), _)->
Some(value)
| Node (_, _, _, l, r)->
min l
Then we continue to code the delete logic:
let rec del value = function
| Leaf(color) ->
failwith "RBT delete failed because x is not in the tree"
| Node (color, y, _, a, b) as s ->
if value < y then balance(color, y, 0, del value a, b)
elif value > y then balance(color, y, 0, a, del value b)
else
match (a, b) with
| (Leaf(Black), Leaf(Black)) -> // without non-leaf children
Leaf(Black++color)
| (Leaf(Black), Node (nc, nv, size, nl, nr))
| (Node (nc, nv, size, nl, nr), Leaf(Black)) -> // with a single child
Node (color++nc, nv, size, nl, nr)
| (l, r) ->
//find the successor (smallest element in a right child),
//replace the key with the successor's
//and delete relevant node
match (min r) with
| Some(v) ->
balance(color, v, 0, l, del v r)
| None ->
failwith "impossible: can't find the successor"
The hard part is how to balance the tree after the deletion of the node. If we delete a black node, then Property 3 cannot hold anymore. So we must make rotations and do some rearrangements on colors to make Property 3 to hold again.
Think this problem in another way: after the deletion of a Black node and we connect its single child or leaf node into it, the node becomes darker. Conceptually Property 3 still holds if we think the node has two “Black”s in it. We mark this node as DoubleBlack and the task of balance is to eliminate this DoubleBlack node!
I defined an operator ++ to plus two colors:
let (++) color1 color2 =
match color1, color2 with
| Red, Black
| Black, Red ->
Black
| Black, Black ->
DoubleBlack
| _, _ ->
Red
Let’s define the invariant for the balance function as follows: no node under pv is DoubleBlack.
Consider pv is the root of the subtree, and its left child is rooted at x, which is a DoubleBlack. Let’s consider all the cases for its right child. (After this is done, then we can work out when x is located as the right similarly.)
Case 1. If pv is black and its right child rv is red. Then do a left-rotation and make the DoubleBlack node x one level down (so that we reduce the problem):
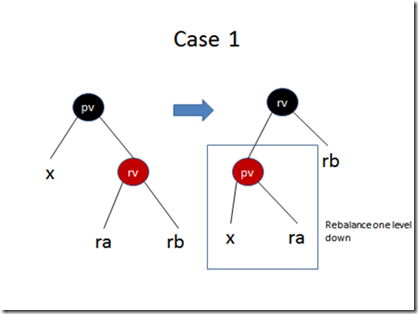
(notations in the picture: nodes in circle are single nodes with colors, blue represents either red or black; a symbol represents a tree rooted at the symbol, for some cases the colors of the symbols are also noted.)
Case 2: If pv is of anycolor, and its right child is black. The three sub cases are shown below:
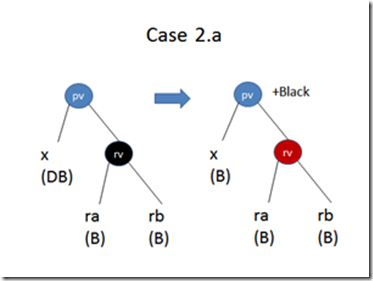
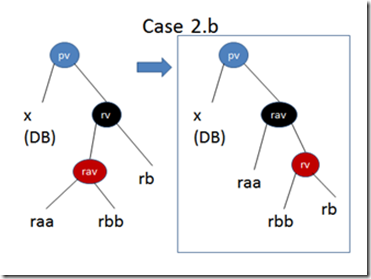
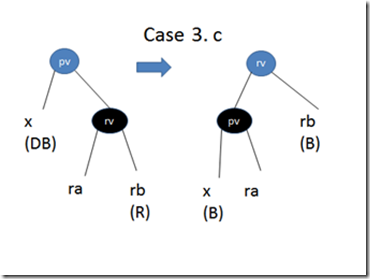
And the balance procedure is as follows:
let rec balance = function
// invariant: the two children rooted at node pv have same "black" depth
// but the root node itself may become a "double" black node
| Black, pv, _, x, Node (Red, rv, size, ra, rb) when (isDoubleBlack x)-> // case 1
balance(Black, rv, 0, balance(Red, pv, 0, x, ra), rb) // do left-rotate and continue balance
| pc, pv, _, x, Node (Black, rv, size, ra, rb) when (isDoubleBlack x)-> // case 2.a 2.b and 2.c
if isBlack ra && isBlack rb then // 2.a: reduce a black on both side
let tempNode=Node (Red, rv, size, ra, rb)
Node (pc++Black, pv, (getSize x tempNode)+1, blackify x, tempNode) // reduces the double node to root
elif isBlack rb then // 2.b: do a right rotation in the right child, so rb becomes red and recudes to the "else" case
match ra with
| Node (_, rav, _, raa, rbb)->
let tempNode1= Node (Red, rv, (getSize rbb rb)+1, rbb, rb)
let tempNode2=Node (Black, rav, (getSize raa tempNode1)+1, raa, tempNode1)
balance(pc, pv, 0, x, tempNode2)
| _->
failwith "impossible error"
else // 3.c
let tempNode=Node (Black, pv, (getSize x ra)+1, blackify x, ra)
Node (pc, rv, (getSize tempNode rb)+1, tempNode, blackify rb)
// when doubleblack x is on the right
| Black, pv, _, Node (Red, lv, _, la, lb), x when (isDoubleBlack x)->
balance(Black, lv, 0, la, balance(Red, pv, 0, lb, x))
| pc, pv, _, Node (Black, lv, size, la, lb), x when (isDoubleBlack x)->
if isBlack la && isBlack lb then
let tempNode=Node (Red, lv, (getSize la lb)+1, la, lb)
Node (pc++Black, pv, (getSize tempNode x)+1, tempNode, blackify x)
elif isBlack la then
match lb with
| Node (_, _, lbv, lba, lbb)->
let tempNode1=Node (Red, lv, (getSize la lb)+1, la, lba)
let tempNode2=Node (Black, lbv, (getSize tempNode1 lbb)+1, tempNode1, lbb)
balance(pc, pv, 0, tempNode2, x)
| _->
failwith "impossible error"
else
let tempNode=Node (Black, pv, (getSize lb x)+1, lb, blackify x)
Node (pc, lv, (getSize la tempNode)+1, blackify la, tempNode)
| a, b, _, c, d->
Node (a, b, (getSize c d)+1, c, d)
Remember that this balance only balances the two children of any tree. Thus the root can still be DoubleDark (similar case in insert). We need a final check on the root:
match del x t with
| Node (_, y, size, a, b) ->
Node (Black, y, size, a, b)
| Leaf _ -> Leaf(Black)
Validation for the implementation
It is important to have some test to verify the correctness of the above implementation. My idea is to do some random insertions and deletions, and then after each insertion or deletion, check whether the tree still holds the three properties.
The validate function is given below:
let validate t =
let rec validate = function
| Leaf Black -> true, 0
| Leaf DoubleBlack ->
printfn "DoubleBlack in a Leaf node"
false, 0
| Leaf Red ->
printfn "Red in a Leaf node"
false, 0
| Node (Black, _, _, a, b) ->
let lr, ln = validate a
let rr, rn = validate b
lr && rr && (ln = rn), ln + 1
| Node (Red, _, _, a, b) ->
match a, b with
| Node (Red, _, _, _, _), _
| _, Node (Red, _, _, _, _) ->
let lr, ln = validate a
printfn "Red-Red in a tree"
false, ln
| _ ->
let lr, ln = validate a
let rr, rn = validate b
lr && rr && (ln = rn), ln
| Node (DoubleBlack, _, _, a, _) ->
let lr, ln = validate a
printfn "DoubleBlack in an internal node"
false, ln
match t with
| Leaf Black -> true, 0
| Leaf _ -> false, 0
| Node (Black, _, _, _, _) ->
validate t
| Node (Red, _, _, _, _)
| Node (DoubleBlack, _, _, _, _) ->
printfn "root must be Black"
false, 0
I did use the above test case to catch one bug in the implementation, the original code for the final deletion step is:
match del x t with
| Node (_, y, size, a, b) ->
Node (Black, y, size, a, b)
| t -> t
This code has a bug that when the tree is deleted to empty, its representation is Leaf (DoubleBlack) rather than Leaf(Black)!
I did a performance test against with F#’s set, which uses AVL tree:
// Fisher-Yates shuffle
let randperm n =
let p = Array.init n (fun i -> i)
let r = new System.Random(1)
for i=n-1 downto 1 do
let j = r.Next(i+1) // random number 0 <= j <= i
let tmp = p.[j]
p.[j] <- p.[i]
p.[i] <- tmp
p
let lst = randperm 1000000 |> Seq.toList
let rb = RBTree.ofList lst |> ignore
open Microsoft.FSharp.Collections
let av = Set.ofList lst |> ignore
//timing on a AMD E-350 Netbook (1.6 GHz)
// Real: 00:00:44.635, CPU: 00:00:44.694, GC gen0: 218, gen1: 61, gen2: 4
//
// val rb : unit = ()
//
// >
// Real: 00:00:17.448, CPU: 00:00:18.766, GC gen0: 76, gen1: 20, gen2: 2
//
// val av : unit = ()
//
As we can see, for a large set with one million elements, my implementation costs about two times of that of AVL tree in F# Core library. That was not bad. I shall devote more time into performance and see if we can do more improvement. One optimization is to reduce redundant tree node allocation.
Tree traversal
Let’s talk some interesting stuff about tree traversal at last. I did implement some traversal functions:
let rec map f = function
| Leaf _ as l -> l
| Node (color, x, size, l, r) -> Node (color, f x, size, map f l, map f r)
let rec iter f = function
| Leaf _ -> ()
| Node (color, x, size, l, r) ->
iter f l
f x
iter f r
let rec fold f t acc =
match t with
| Leaf _ -> acc
| Node (color, x, size, l, r) -> fold f l (f x (fold f r acc))
They are straightforward recursive functions, and not tail-recursive. For a balanced tree like red black tree, tail-recursive is not important because the tree does not go too deep (a tree with 1 to 1000000 in it has a depth of 26). But it is just fun to make tem tail-recursive by using continuations. The standard accumulating variable trick does not work here because we have two recursive calls.
Let’s write the tail-recursive form of map function:
let map2 f t =
let rec map f t k =
match t with
| Leaf _ as l -> k l
| Node (color, x, size, l, r) ->
map f l (fun lmap ->
map f r (fun rmap -> k (Node(color, f x, size, lmap, rmap))))
map f t (fun x -> x)
We can also use a Monad to abstract the continuation pattern out:
type Cont<'a,'r> = ('a -> 'r) -> 'r
type ContBuilder() =
member x.Return (a):Cont<'a,'r> = fun k -> k a
member x.Bind (c:Cont<'a,'r>, f:'a -> Cont<'b,_>) =
(fun k -> c (fun a -> f a k))
member this.Delay(f) = f()
let cont = ContBuilder()
let map3 f t =
let rec map f = function
| Leaf _ as t -> cont { return t }
| Node (color, x, size, l, r) ->
cont {
let! lm = map f l
let! rm = map f r
return Node (color, f x, size, lm, rm)
}
map f t (fun x -> x)A note on <'a when 'a:comparison>
In our definition of the Red Black Tree:
type RBTree<'a when 'a:comparison> =
| Node of Color * 'a * int * RBTree<'a> * RBTree<'a>
| Leaf of Color
The type signature has an ad hoc construct: when ‘a: comparison. Actually the only other constraint on ‘a is equality. F# only supports these two type constraints.
Type constraints behave like type classes in Haskell. :equality is Eq, :comparison is Ord. However, type classes in Haskell are much flexible.
Details could be found on this blog article by Don Syme.
Summary
In this article, I have implemented a functional Red Black Tree with dynamic order statistics. The tree is complete and has been well tested. Before any performance tuning, the running speed of it is within a small factor (2-3) of the AVL tree in F# Core library.
This article shows many important features of functional programming: 1) pattern matching and algebraic data types help implement complex data structures; 2) recursion is everywhere and the correctness of the program could be proved by inductive reasoning; and finally 3) a light introduction to tree traversal and continuation and Monad in F#.
![]()




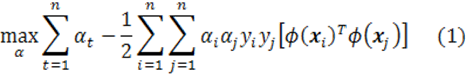
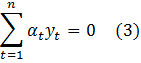

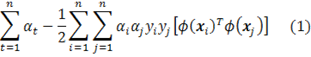
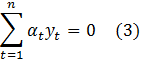
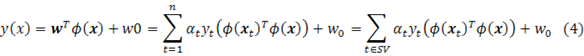
![clip_image002[5] clip_image002[5]](http://lh4.ggpht.com/_4bFBK2BKrQI/TWYLYO2ZIXI/AAAAAAAABHQ/8Y_8SOkg4xM/clip_image002%5B5%5D_thumb%5B1%5D.png?imgmax=800)